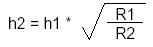
Last modified: 2004-09-18 by phil nelson
Keywords: flag area |
Links: FOTW homepage |
search |
disclaimer and copyright |
write us |
mirrors
See also:
We start with the basics. Lets have a flag, for now let us consider it rectangular with the height equal h and length equal l, that makes it area equal A = h * l. Let us define the ratio as R = l/h.
The requirement that two flags displayed together have equal area could then be made so:
A1 = h1 * l1 or A1 = (h12) * R1
and similarly
A2 = h2 * l2 or A2 = (h22) * R2
A1 = A2 gives us easily that the height of the second flag should be:
That was easy, but this does not take into account the visual "feeling" that is effect of the flag flying in the wind. Now until here things were quite clear mathematically, but henceforward I take some assumptions and hypothesis.
Let us assume that the area of a flag flying in the wind as perceived by the observer depends only on the amount of the wind blowing. The stronger the wind the lesser the "wrinkling" and therefore the "virtual area" would be close to the area of the still flag on surface. The simplest function to emulate this following the natural laws would be exponential one, like this:
A' = A * f(v) = A * (1-e(-av))
where v is the speed on the wind and a is the "perception coefficient"; - a value that would have to be experimentally determined.
For large values of the perceptions coefficient, the value of virtual area A' approaches the still flag area A.
The answer to the practical question how "big" a flag one should hoist beside the first flag so they appear the same, what interests us is the size of the hoist of the second flag:
The wind speed is the same in both flags, of course. The last expression mi